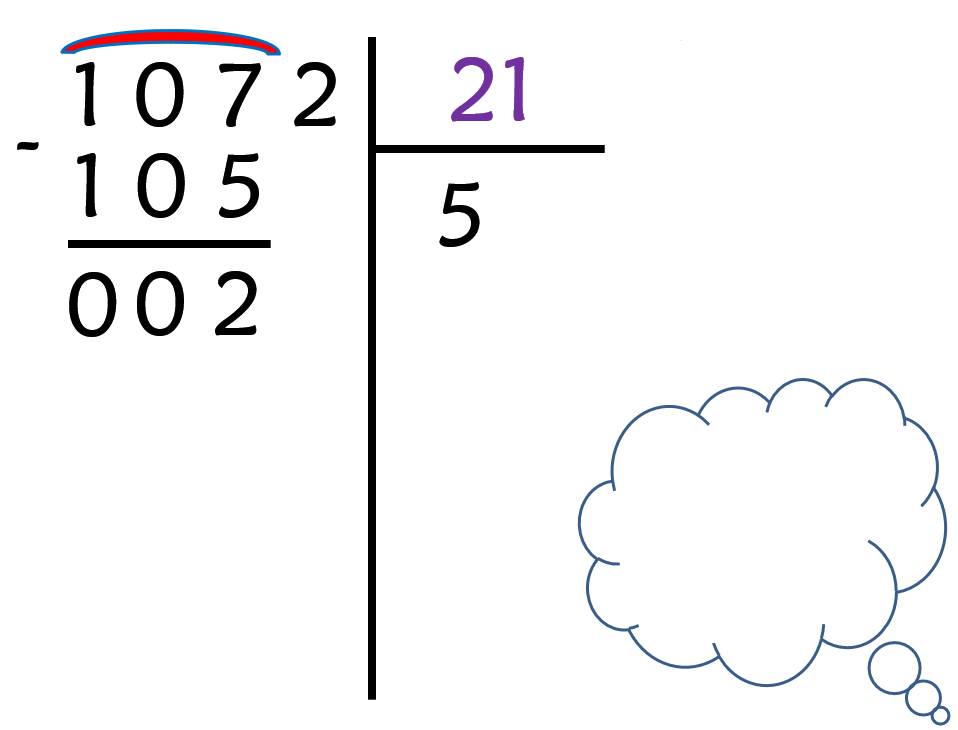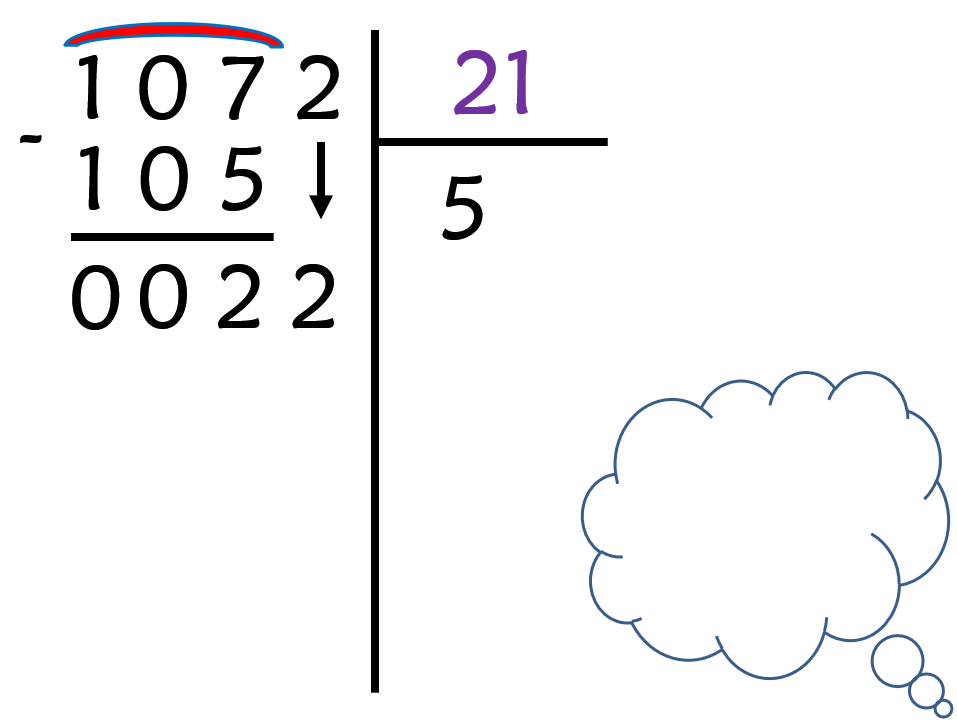Nous allons voir les différentes étapes qui vous permettront de poser une division par un nombre à deux chiffres.
Dans cet article, nous n’irons pas dans la partie décimale au quotient. Cette possibilité est traitée dans un autre article.
La description sera illustrée avec l’opération 1 072 ÷ 21
0 – Construire la table
La seule différence entre une division par un nombre à un chiffre et une division par un nombre à deux chiffres, c’est la table du diviseur !
– Si on divise par 6, on connait généralement la table de 6 (ou on peut facilement la trouver).
– Si on diviser par 21, on ne connait pas la table, et il est plus difficile de la trouver.
![]() Nous vous conseillons donc de commencer par créer cette table, de tête ou à l’aide d’une calculatrice !
Nous vous conseillons donc de commencer par créer cette table, de tête ou à l’aide d’une calculatrice !

1 – Poser l’opération
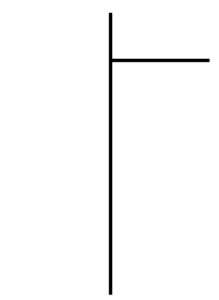
- Commencez par tracer la potence (ou la chaise).

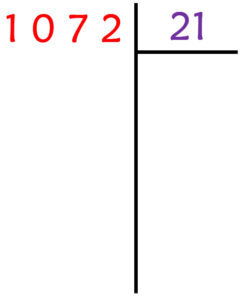
- Placez le dividende en haut à gauche, et le diviseur en haut à droite.

2 – Réaliser l’opération
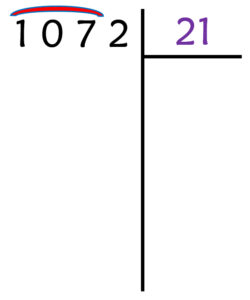
- Commencez l’opération en prenant les trois premiers chiffres : 107.

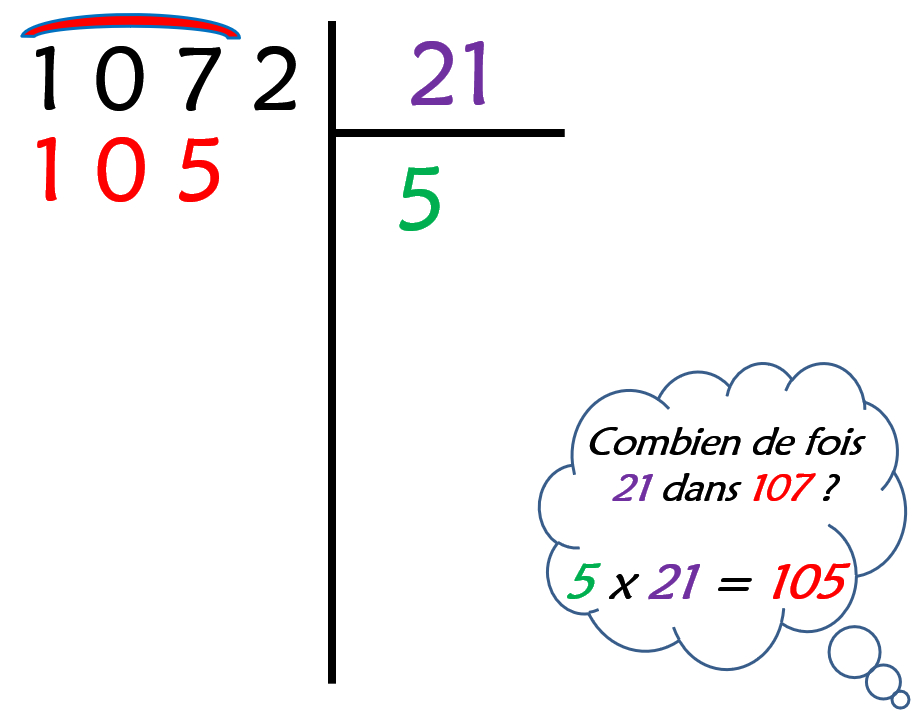
Quelle question se pose-t-on ?Dans 107 combien de fois 21 ? |
- Cherchez dans 107, combien de fois 21 : 5 x 21 = 105. Écrivez les informations dans l’opération :
– Le 5 au quotient
– Le 105 en dessous du 107.

- Effectuez la soustraction 107 – 105.
 C’est logique : dans 107, on prend 105 (5 paquets de 21), on doit donc les enlever en faisant une soustraction !
C’est logique : dans 107, on prend 105 (5 paquets de 21), on doit donc les enlever en faisant une soustraction !

- Descendez le 2 à côté du 2, pour pouvoir continuer l’opération.

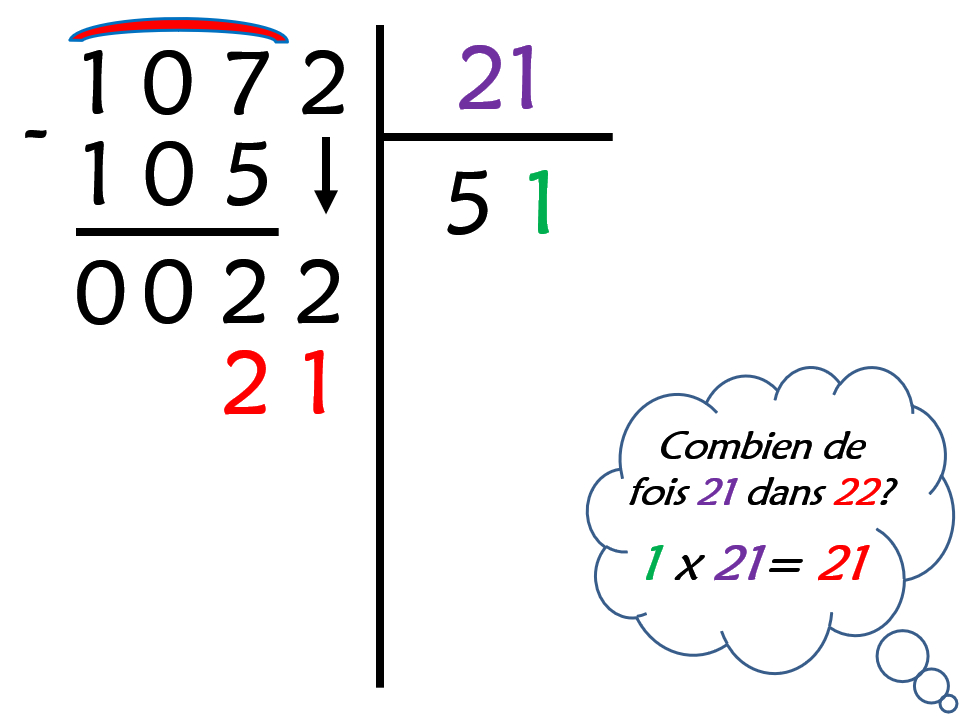
- Cherchez dans 22, combien de fois 21 : 1 x 21 = 21. Écrivez les informations dans l’opération :
– Le 1 au quotient
– Le 21 en dessous du 22.

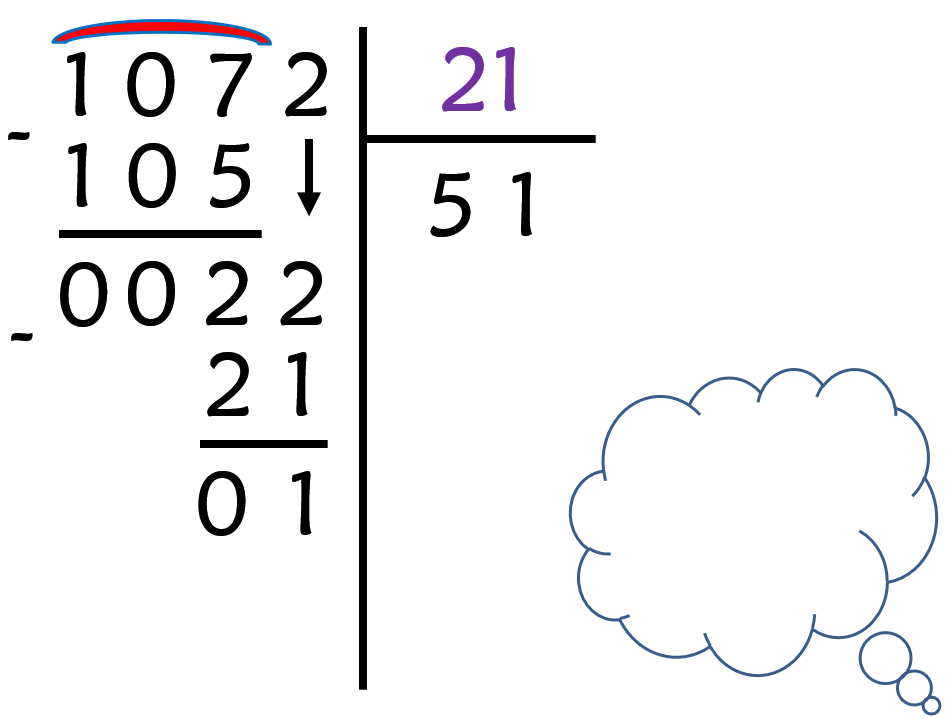
- Effectuez la soustraction 22 – 21.

- Il n’y a plus de chiffre à descendre : votre opération est à présent terminée !
1 072 ÷ 21 = 51 r 1
Quand on divise 1 072 par 21, on obtient des parts de 51, et il reste 1 qu’on ne peut pas diviser (sauf à aller dans la partie décimale, ce qui est traité dans un autre article…).